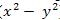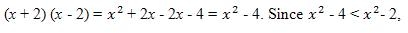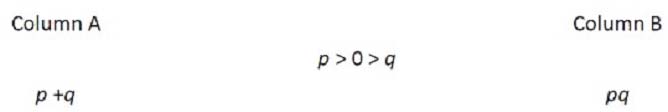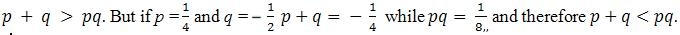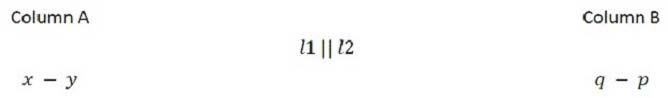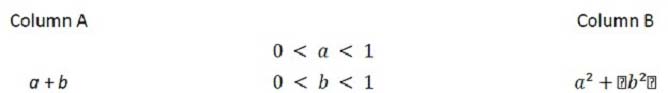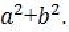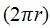Section Two Quantitative
Here you have the best Test Prep GRE Section 2 Quantitative practice exam questions
- You have 49 total questions to study from
- Each page has 5 questions, making a total of 10 pages
- You can navigate through the pages using the buttons at the bottom
- This questions were last updated on May 15, 2025
- This site is not affiliated with or endorsed by Test Prep.