If the radius of the circle above is equal to the chord AB, then what is the value of?
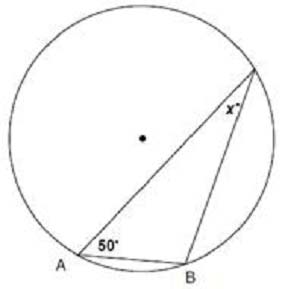
If the radius of the circle above is equal to the chord AB, then what is the value of?

Given that the radius of the circle is equal to the chord AB, triangle OAB is an isosceles triangle (OA = OB = AB). In such a triangle, the angle at the center (angle OAB) is supplementary to twice the given angle at A (which is 50 degrees) because the angle subtended by the chord at the circumference is half the angle subtended at the center of the circle for the same arc. Therefore, 2 * 50 = 100 degrees is the angle at the center. Since the total angle around point O is 360 degrees and the angle at A + angle at B (which are both equal) = supplementary to the central angle, the remaining angle at B within the triangle will also be 50 degrees as angle at A and B. Therefore, x = 50 degrees.
The question is missing .. What is the value of what?