What is the area of the trapezoid above if AB = BC = CD = 6, and AD = 12?
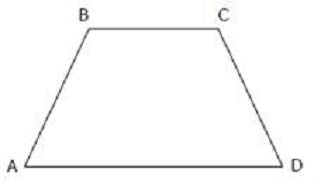

What is the area of the trapezoid above if AB = BC = CD = 6, and AD = 12?


The area of a trapezoid is calculated by the formula: Area = 0.5 * (a + b) * h, where 'a' and 'b' are the lengths of the two parallel sides (bases) and 'h' is the height. For this trapezoid, AD is the longer base (12 units), and BC is the shorter base (6 units). A trapezoid with legs of equal length (AB = CD = 6 units) forms two right triangles with height 'h' and hypotenuse 6. The legs of these triangles (forming a right angle) are equal with 'h' as one leg and the other leg half the difference between AD and BC (3 units). Using the Pythagorean theorem, h = sqrt(6^2 - 3^2) = sqrt(36 - 9) = sqrt(27) = 3sqrt(3). Therefore, the area = 0.5 * (12 + 6) * 3sqrt(3) = 9 * 3sqrt(3) = 27sqrt(3). Hence, the correct option is 9√3.
Answer choices are wrong .. The area should be 27*3^2