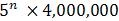
If n is an integer and -
what is the least possible value of n ?
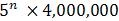
If n is an integer and -
what is the least possible value of n ?
To determine the least possible value of n for which 5^n is greater than 4,000,000, we need to solve the inequality 5^n > 4,000,000. We can use logarithms to find the value of n. Taking the base 10 logarithm on both sides of the inequality, we get log(5^n) > log(4,000,000), which simplifies to n * log(5) > log(4,000,000), or n > log(4,000,000) / log(5). Evaluating the logarithms: log(4,000,000) is approximately 6.60206 and log(5) is approximately 0.69897. Dividing these values gives n > 6.60206 / 0.69897, which is approximately 9.44. Since n must be an integer, the smallest possible value of n is 10.
The question is wrong - Here is the correct one "If n is an integer and 5^n > 4,000,000, what is the least possible value of n? "