For the data shown here which statement(s) are true? (Note: There are 2 correct answers).
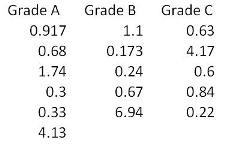
For the data shown here which statement(s) are true? (Note: There are 2 correct answers).

The dataset shows a range of values for three grades. With visible skewness and considerable differences among values, especially for Grade B, it is likely that the distributions of these samples are not normal. Therefore, we can confidently conclude with more than 95% confidence that these samples are from non-normal distributions. Given that the data is not normally distributed and we want to compare the central tendencies of these three samples, Mood's Median test is appropriate because it does not assume normal distribution of data. One-way ANOVA, on the other hand, requires the data to be normally distributed, which is not the case here.
I THINK "BD" are the correct answers. If the populations being sampled are normally distributed or each sample is greater than 20, use the one-way ANOVA. If the populations being sampled are severely skewed and you have small samples, use the Mood's median or the Kruskal-Wallis test. Although the Mood’s median test does not require normally distributed data, that does not mean that it is assumption free. The assumptions of Mood’s median test are that the data from each population is an independent random sample and the population distributions have the same shape.