FILL BLANK -
Refer to the confusion matrix:
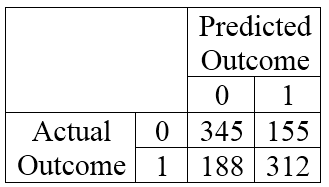
An analyst determines that loan defaults occur at the rate of 3% in the overall population. The above confusion matrix is from an oversampled test set (1 = default).
What is the sensitivity adjusted for the population event probability?
Enter your answer in the space below. Round to three decimals (example: n.nnn).
To find the sensitivity (recall) adjusted for the population event probability, we need to follow these steps: 1. Calculate the sensitivity from the confusion matrix: Sensitivity (Recall) = True Positives / (True Positives + False Negatives) From the confusion matrix: True Positives (TP) = 312 False Negatives (FN) = 188 Sensitivity = 312 / (312 + 188) = 312 / 500 = 0.624 2. Adjust the sensitivity for the population event probability: The analyst determines that loan defaults occur at the rate of 3% in the overall population. Adjusted Sensitivity = Sensitivity * Population Event Probability = 0.624 * 0.03 = 0.01872 After adjustment, the sensitivity for the given population event probability is 0.019 (rounded to three decimals).
answer is 312/500=0.624
and adjustment of 3%?
Why is .624 (the true sensitivity) the correct answer? I've seen others state you reduce the TP by 3% and then re-calculate sensitivity which gives the answer currently showing of .617.
The answer is: Adj_Sensitivity = N * PriorProb * Sensitivity = 1000 * 0.03 * 0.624 = 18.72
I think it is: n*p1*sensitivity=500*0.03*0.624=9.36
It's 312/(188+312)