Refer to the confusion matrix:
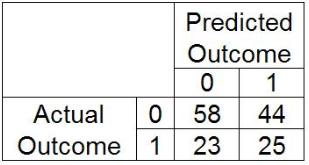
Calculate the accuracy and error rate (0 - negative outcome, 1 - positive outcome)
Refer to the confusion matrix:

Calculate the accuracy and error rate (0 - negative outcome, 1 - positive outcome)
To calculate the accuracy and error rate from the confusion matrix, use the following formulas: Accuracy = (True Negatives + True Positives) / Total Population and Error Rate = (False Positives + False Negatives) / Total Population. From the given confusion matrix, True Negatives (TN) = 58, True Positives (TP) = 25, False Positives (FP) = 44, and False Negatives (FN) = 23. The total population (N) is the sum of all four values: 58 + 44 + 23 + 25 = 150. Therefore, the accuracy is (58 + 25) / 150 = 83/150, and the error rate is (44 + 23) / 150 = 67/150.
the correct answer is D
Agree with D. https://towardsdatascience.com/taking-the-confusion-out-of-confusion-matrices-c1ce054b3d3e
The correct answer is D: Accuracy = ( TN + TP ) / N Error Rate = ( FP + FN ) / N