Refer to the exhibit.
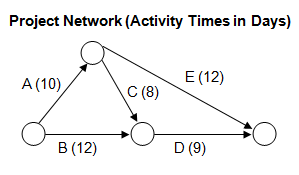
The figure below shows the network diagram for the activities of a large project. What is the shortest number of days in which the project can be completed?
Refer to the exhibit.

The figure below shows the network diagram for the activities of a large project. What is the shortest number of days in which the project can be completed?
To determine the shortest number of days in which the project can be completed, we need to find the critical path, which is the longest path through the network. The possible paths and their durations are: A to B to D, which is 10 + 12 + 9 = 31 days, A to C to D, which is 10 + 8 + 9 = 27 days, and A to E, which is 10 + 12 = 22 days. The longest duration among these paths is 27 days for the A to C to D path. Therefore, the shortest number of days in which the project can be completed is 27 days.
The longest path is ACD. You can't complete the project if C is not completed.
Activity: B-D= 12+9=21 Activity A-C-D= 10+8+9=27 Activity A-E= 10+12=22 Critical Path= Longest Path among all possible ways to reach final destination (which is 27 days for A-C-D)
Don't confuse path and duration.
I didnt get it? Illustrate plz
I don't get it either. please explain
Tricky. Apparently, the shorter should consider passing thru all nodes, without jumping any of them
at each node, choose the shorter of the options and follow that as the shortest path
I don't understand how they calculated it
Critical Path is the longest path among the three paths, which is ACD. I got it in less than a minute