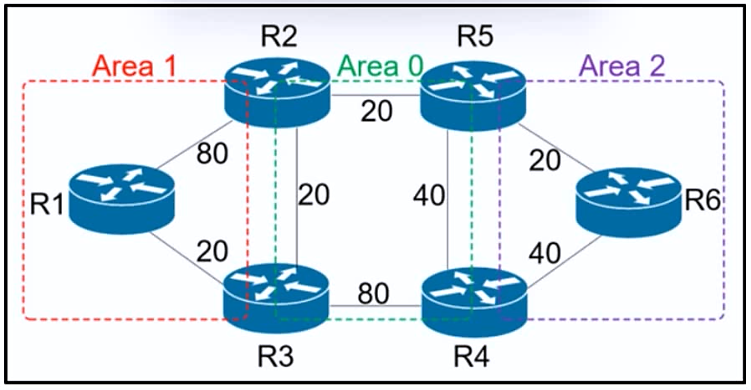
Refer to the exhibit. R6 should reach R1 via R5>R2>R1. Which action resolves the issue?

Refer to the exhibit. R6 should reach R1 via R5>R2>R1. Which action resolves the issue?
To ensure R6 reaches R1 via R5 > R2 > R1, we need to make the current least-cost path (R5 > R2 > R3 > R1) less favorable. By increasing the cost between R2 and R3 to 61, the total cost of the path through R3 becomes higher (20+61=81), making the path via R5 > R2 > R1 (20+20=40) the preferred route. Therefore, the correct action is to increase the cost between R2 and R3 to 61.
Agree with Demir11's calculation.
I detest how these are worded sometimes. Technically speaking, if you increase the cost TO 61, then the cost of the link = 61 (in which case, it doesn't use the R1-R2 link). However, if you increase the cost BY 61, then the cost of the link = 81 (20+61). This is just splitting hairs over semantics, but the question is worded incorrectly.
Increase cost BY 61. Keyword BY, not TO 61. When you increase BY 61, total becomes 81 which is what you want to achieve.
Basically due to the lowest cost the path it is taking before the change is R6-R5-R2-R3-R1 Increasing the cost by 61 makes the total cost 81>80 so it will prefer R1
can someone explain this?
On each suggestion, try replace the cost with the suggested one, then sum from R6 all the way to R1. You'll find that answer C presents the lowest cost possible to choose the path R5>R2>R1
a)6-5-2-1=82 6-5-2-3-1=42 b)6-5-2-1=120 6-5-2-3-1=111 c)6-5-2-1=120 6-5-2-3-1=141 d)6-5-2-1=81 6-5-2-3-1=89
The calculation for d is wrong or probably a typo, 6-5-2-3-1=80. Thus the solution is C.
See the answer provided by sol_ls95. I agreed with the user.
What sol_ls95 said is incorrect. This would make 6-5-2-1= 81 and 6-5-2-3-1=80.
C is corerct